Die Hard Jug Puzzle I

From jug puzzles to Bézout's Identity

June 15 / 2021 ____________________

Suppose you have two jugs that hold 7 gallons and 10 gallons of liquid respectively. Let’s further suppose that there are no visible markings on the jug, thus making it impossible to eyeball the volume of liquid inside. Now, how would you fill up these jugs so that they sum to exactly 12 gallons? This is the exact problem Detective McClane and Electrician Carver faced in the movie Die Hard 3, except for a much dire consequence—the resulting volume must be within an ounce to target or a ticking bomb goes off. Nonetheless, the jug puzzle in the movie—to make 4 gallons out of 3 and 5-gallon-jugs—seems to be a simpler variant. Therefore, a sensible approach is to toy with the simpler version and hope that it can generalize to the more difficult one.

Given a 5-gallon and a 3-gallon-jug, how can you fill them with exactly 4 gallons of liquid?

With a bit of trial and error, we can first fill up the 5-gallon-jug, then pour it into the 3-gallon-jug until filled, leaving 2 gallons of liquid behind. We can then empty the 3-gallon-jug and into it pour the remaining 2-gallon-leftover. Notice that the 3-gallon-jug is only a gallon short of full. Now, all that's left is to refill the 5-gallon-jug and continue to pour the liquid into the 3-gallon-jug until filled. In other words, we have poured away 1 gallon from 5 gallons, leaving behind exactly 4 gallons. Phew! Another day saved! But we are not quite done yet. Can you come up with a different way of filling the jugs to get 4 gallons? This time, we will start by filling up the 3-gallon-jug, then empty it into the 5-gallon-jug. Now, let's refill the 3-gallon-jug and, similar to the previous solution, carefully pour away another 2 gallons to fill up the 5-gallon-jug. In the 3-gallon-jug currently sits exactly one gallon of liquid. Let's empty the 5-gallon-jug to make room for the 1-gallon-leftover. With one gallon secured, we can finally refill the 3-gallon-jug to get a total sum of 4 gallons.

That was not too thorny. But how can these two solutions help solve our original puzzle? What are steps taken that lead to the target? Can an algebraic representation generalize our solution to all other jug puzzles? Let's find out. Let

x_m, y_m

denote the capacity of the two jugs, where

x_m > y_m

. Let

x

y

be the current volume of liquid inside the two jugs, where

x in [0, x_m], y in [0, y_m]

In Die Hard 3, the jugs are 3 and 5-gallon respectively, or $x_m = 5, y_m = 3$ . Now, let these symbols represent the steps in the two solutions.

Solution 1:

step	physical steps	symbolic step	volume
1	fill 5GL jug	$(x, y) = (x_m, 0)$	(5, 0)
2	pour 5GL jug into 3GL jug	$x = x - y_m$ , $y = y_m$	(2, 3)
3	empty 3GL jug, into it pour 2GL leftover	$(x, y) = (0, x)$	(0, 2)
4	refill 5GL jug	$(x, y) = (x_m, y)$	(5, 2)
5	pour 5GL jug into 3GL jug uitil filled	$x = x_m - (y_m - y)$ , $y = y_m$	(4, 3)
6	empty 3GL jug	$(x, y) = (x, 0)$	(4, 0)

Solution 2:

step	physical steps	symbolic step	volume
1	fill 3GL jug	$(x, y) = (0, y_m)$	(0, 3)
2	empty 3GL jug into 5GL jug	$(x, y) = (y, 0)$	(3, 0)
3	refill 3GL jug	$(x, y) = (x, y_m)$	(3, 3)
4	pour 3GL jug into 5GL jug until filled	$x = x_m$ , $y = y_m - (x_m - x)$	(5, 1)
5	empty 5GL jug, into it pour 1GL leftover	$(x, y) = (y, 0)$	(1, 0)
6	refill 3GL jug	$(x, y) = (x, y_m)$	(1, 3)

With the power of algebra, we can discard the numbers and focus on the symbols only. To help us generalize better, we can extract common operations used across the solutions as the following:

Note: these operations are valid if $x in [0, x_m]$ , $y in [0, y_m]$ .

id	operation	symbolic operation
a	fill empty x	$(x, y) = (x_m, y)$
b	fill empty y	$(x, y) = (x, y_m)$
c	pour away x to fill non-empty y	$x = x_m - (y_m - y)$ , $y = y_m$
d	pour away y to fill non-empty x	$x = x_m$ , $y = y_m - (x_m - x)$
e	pour x into empty y	$(x, y) =begin{cases} (0, x) & x leq y_m (x - y_m, y_m) & x gt y_m end{cases}$
f	pour y into empty x	$(x, y) = (y, 0)$
g	dump x	$(x, y) = (0, y)$
h	dump y	$(x, y) = (x, 0)$

If we think of the volume of both jugs $(x, y)$ as a state of the jug problem, then these operations are means to get from one state to another. For instance, the 4th step in Solution 1 shows an operation: $x = x_m - (y_m - y)$ via which one can get from $(5, 2)$ to $(4, 3)$ . Using states and operations as building blocks, an intuitive representation into which we can transform the problem is a graph.

Graph 1.1

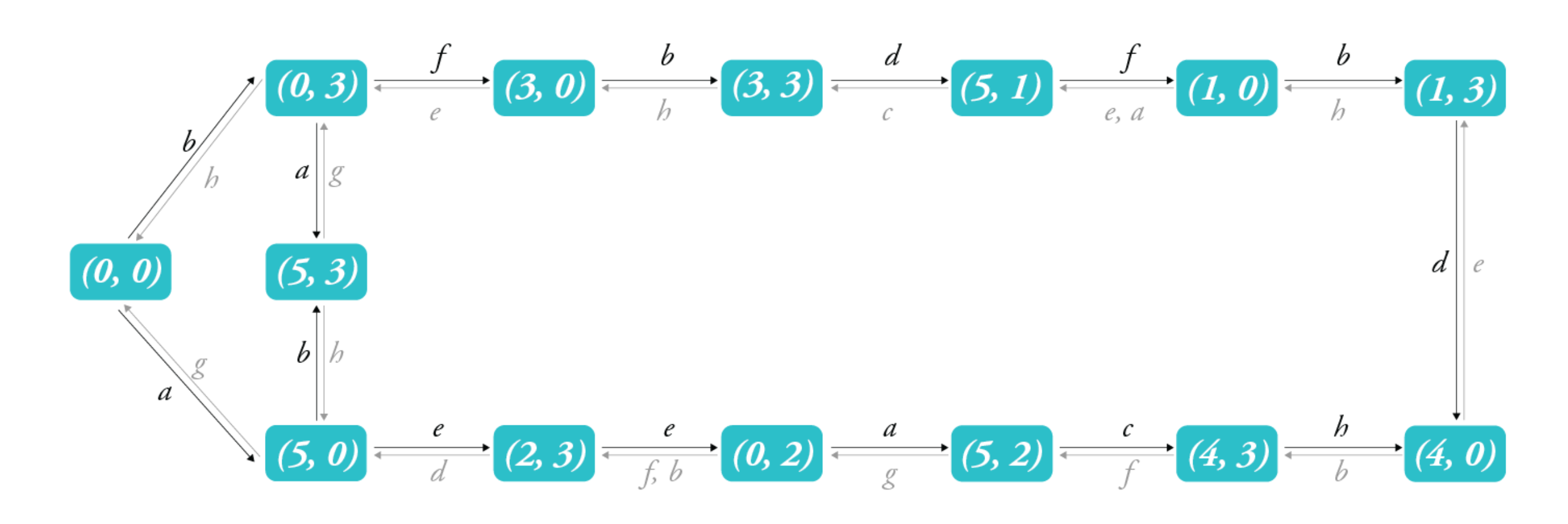
A graph is composed of a set of vertices and edges. In Graph 1.1, the vertices represent the states $(x, y)$ while the edges the allowable operations. Notice that the edges are bidirectional, in other words, the same operation can be reversed such that any given state can reach both of its predecessor and successor. For instance, from state $(1, 0)$ , one can perform operation b to get to $(1, 3)$ , or operation e then a to reverse back to $(5, 1)$ .

Since our target concerns only with the sum $s_i$ = $x_i + y_i$ , we can simplify the above graph by summing each vertex and prunning repeated sums. Graph 1.2 shows a prunned version of Graph 1.1, where edges with more than one operation denote a sequence of operations to be performed in order. Let's take one step further and remove vertices whose $s_i > x_m$ . We are able to do so for the following reasons:

$forall s_j$ where $s_j in (x_m, x_m + y_m]$ ,
$exist s_k$ where $s_k in (0, y_m]$ , such that $s_j = s_k + x_m$ .
$because$ $s_k = s_j - x_m$ .
$s_j - x_m in (x_m - x_m, x_m - x_m + y_m]$ $Longrightarrow s_k in (0, y_m]$

For instance, Let $s_j = 6, s_k = 1$ . $s_j = s_k + x_m = 1 + 5$ . Thus, for any sum $s_i > x_m = 5$ , if we can reach all $s_k in (0, y_m = 3]$ , then we shall reach all $s_j in (5, 8]$ .

Assumption [1]: $forall s_i in (0, y_m], exist (x_i, y_i)$ , such that $s_i = x_i + y_i$ .

Graph 1.2 (L) & Graph 1.3 (R)

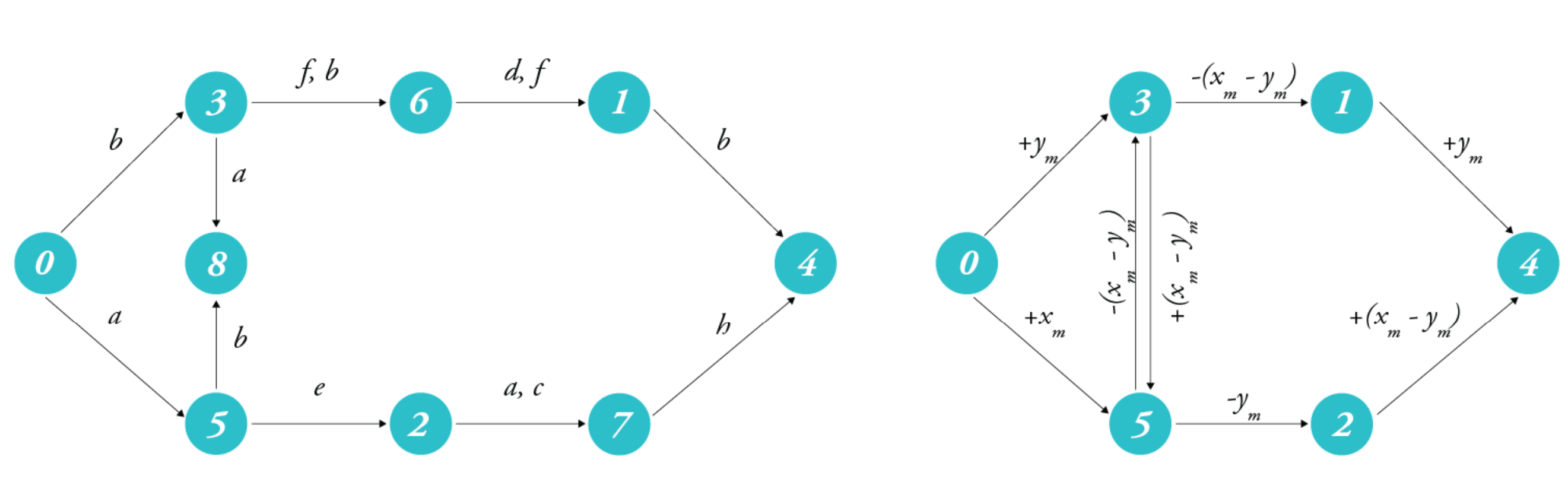
For now, should we take this assumption for granted, Graph 1.2 can be reduced to Graph 1.3. Furthermore, we can truncate the edges threading $s_i$ by combining their sequence of operations. For instance, operations f, b, d, f going through vertex $s_i = 6$ can be reduced to $s_{i+1} = s_i + y_m - x_m$ , while operations a, c, h going through vertex $s_i = 7$ can be simplified to $s_{i+1} = s_i + x_m - y_m$ .

Thus, the distilled graph representation only requires the following operations:

Note: these operations are valid only when $s_{i+1} in [0, x_m + y_m]$ .

symbolic operation
$s_{i+1} = s_i+x_m$
$s_{i+1} = s_i pm y_m$
$s_{i+1} = s_i pm(x_m - y_m)$

Using this new symbolic representation, can you solve the original problem?

Given a 10 and a 7-gallon-jug, how can you fill them with exactly 12 gallons of liquid?

Well, we can start by reformulating the problem statement with our new found representation:

Let $x_m = 10$ , $y_m = 7$ . Perform one operation at a time, show all states in sequence ${s_0, s_1, s_2, ... s_t}$ between $s_0 = 0$ and $s_t = 12$ ?

In this representation, there are no better ways to reach the target than trial and error, so long as the next state $s_{i+1} in (0, x_m + y_m]$ . Let's begin from $s_0 = 0$ . The valid options are $+x_m$ or $+y_m$ . Therefore $s_1$ is either $0 + y_m = 7$ or $0 + x_m = 10$ . For $s_1 = 7$ , the valid options are $s_2 = s_1 pm(x_m - y_m)$ , or $s_2 = s_1 - y_m$ . In the spirit of not repeating seen numbers, we proceed with $s_2 = s_1 - (x_m - y_m) = 4$ . In addition, given Assumption [1], we can further avoid yielding $s_i > x_m$ for we conject that all $s_i$ are reachable by $s_k + x_m$ , where $s_k in (0, y_m]$ .

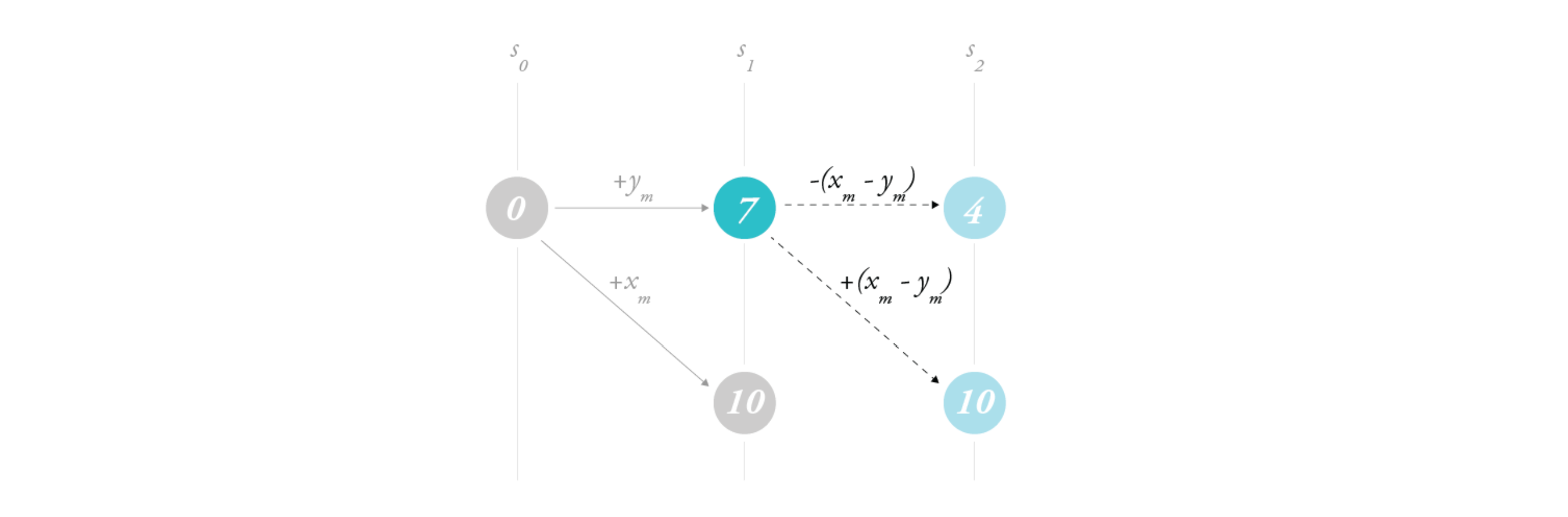
Thus we turn our trial-and-error into the following algorithm:

If we "run" the algorithm in our heads, we get the following result: ${0, 7, 4, 1, 8, 5, 12}$ .

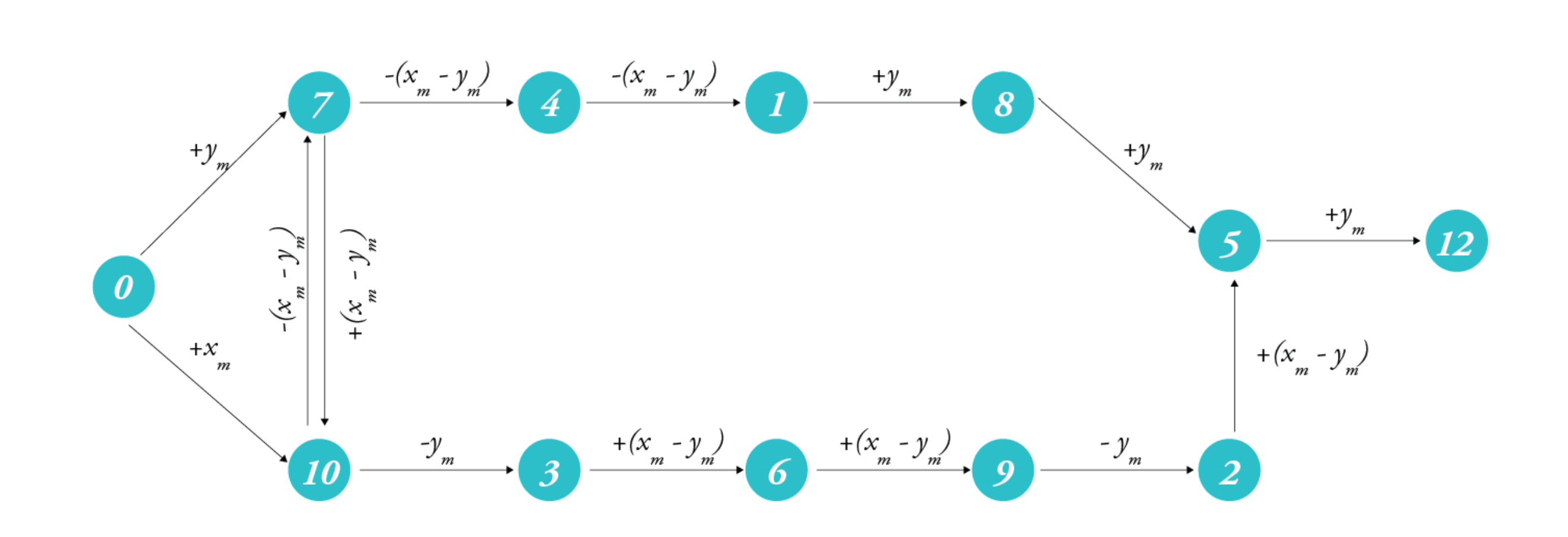
With the trial and error algorithm, it is possible that we will visit all $s_i in (0, x_m], s_i neq s_t$ before we can get to our target $s_t$ . Thus, we can estimate an upper bound $n$ for the worst case that takes n steps to reach the target, where $n = |operations| * x_m$ .

All seems well, except for two minor problems:

The assumption on which our algorithm rests upon has yet to be proven.
Can we do better than trial and error, in other words, can we find an algorithm that takes less steps to get to the target?

To see how we might go about these problems, stay tune for part II.

References:
Eugenia Cheng. "The Perfect Glass of Wine." The University of Sheffield Youtube Channel.
Mathologer. "How not to Die Hard with Math." Youtube Channel.